こんにちは。
この記事では、月刊こども新聞2025年1月号（FMふくやま）に出題した問題について考えていきます！
（今回の記事も、新コースの歩みに関するものではまりません。）

問題

2025年がスタートしましたね。新年といえば、くじを引く機会が多い時期だと思います。今回は、くじに関する問題です。

５本のくじの中にあたりくじが２本、はずれくじが３本あります。この中から次のように２回くじをひきます。
〔１回目〕５本のくじの中から１本引き、あたり、はずれを確認した後、引いたくじをもとにもどしてよくかきまぜる。
〔２回目〕もう一度５本のくじの中から１本引き、あたり、はずれを確認する。
２回くじを引いた結果として、１番起こりやすいと考えられるものを次の①～③から１つ選んでみましょう。

①　２回ともあたり
②　あたりとはずれが１回ずつ
③　２回ともはずれ

答え

１番起こりやすいのは②（あたりとはずれが１回ずつ）です。答えを見て、意外に思った人もいるのではないでしょうか。
ここからは、なぜ②が一番起こりやすいといえるのか、考えていきたいと思います。

考察

2本のあたりくじを、次のように表すことにします。

また、3本のはずれくじを次のように表すことにします。

このとき、くじの引き方の全パターンは次のように図に表すことができます。

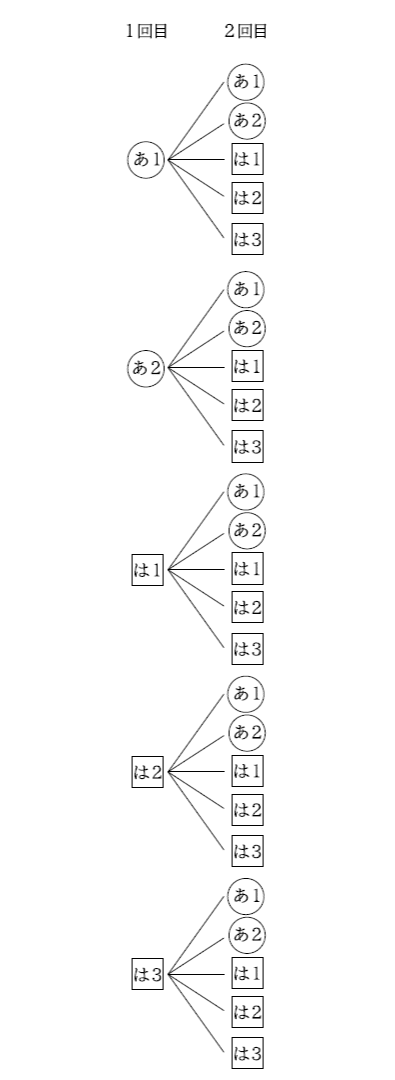
このような図のことを「樹形図」といいます。
数えてみると25通りあることがわかりますが、計算して求めることもできます。１回目のくじの引き方は5通りあり、その1つ1つに対して２回目のくじの引き方は5通りずつあります。したがって、5×5=25（通り）と計算することができるのです。
これら25通りのくじの引き方は、どの場合が起こることも同じ程度に期待されます。（これを数学では「同様に確からしい」といいます）

全25通りのうち、2回ともあたる場合は、次のように図に表すことができます。

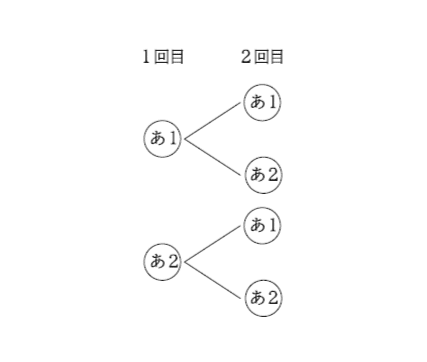
全部で4通りですが、これも先ほどと同じように2×2=4（通り）と、計算することができます。

次に、あたりとはずれが1回ずつとなる場合は、次のように図に表すことができます。

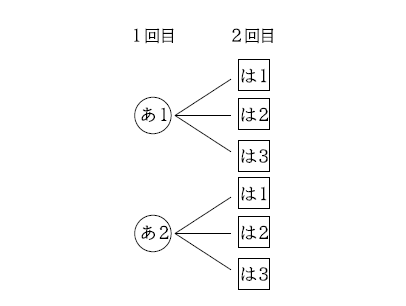
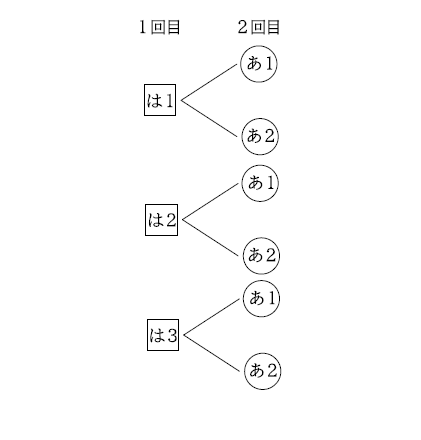
図３の場合は2×3=6（通り）、図４の場合は3×2=6（通り）と計算することができ、合わせて6+6より12通りあることがわかります。

最後に、2回ともはずれる場合は次のように図に表すことができます。

3×3の9通りあります。

まとめると次のようになります。

• くじの引き方は全部で25通り

• 2回ともあたりになるのは4通り

• あたりとはずれが1回ずつになるのは12通り

• 2回ともはずれるのは9通り

以上より、1番起こりやすいのは②の（あたりとはずれが1回ずつ）ということになります。

おわりに

どうでしたか？
今回の考察では、「場合の数」のみを扱いましたが、起こりやすさの程度を表す数「確率」を用いて、さらに詳しく考えることもできます。よければ挑戦してみてくださいね。